LES
What is LES?
Turbulent flows contain eddies with a range of sizes and energies.
In LES we will going to resolve eddies with a mesh.
This is called Large Eddies Simulation, LES.
How do we do LES?
Problem
Of course we can resolve eddies bigger than a mesh using velocity vectors.
But how about eddies smaller than a mesh?
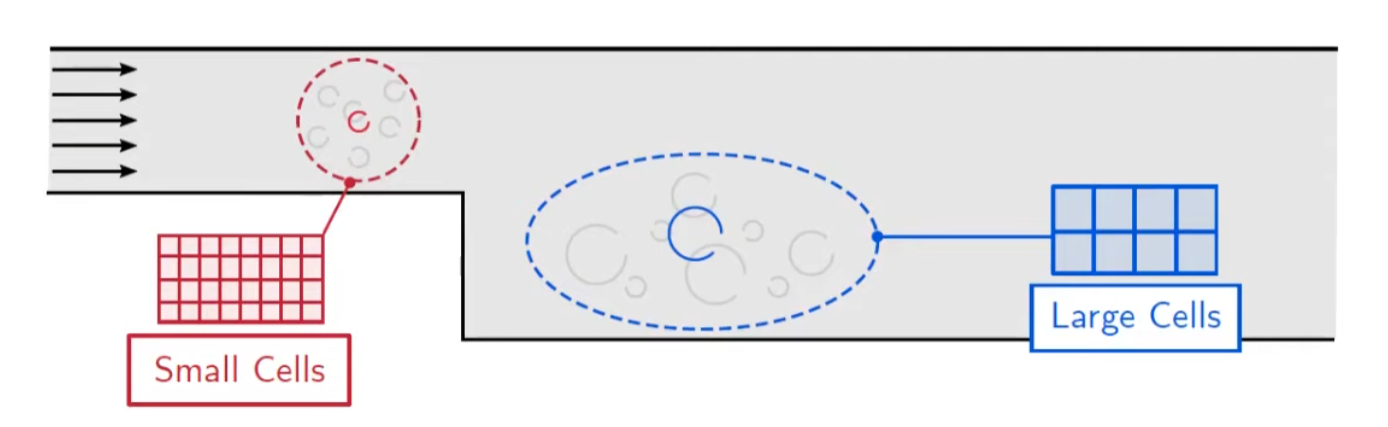
The below picture shows the concept of the problem. 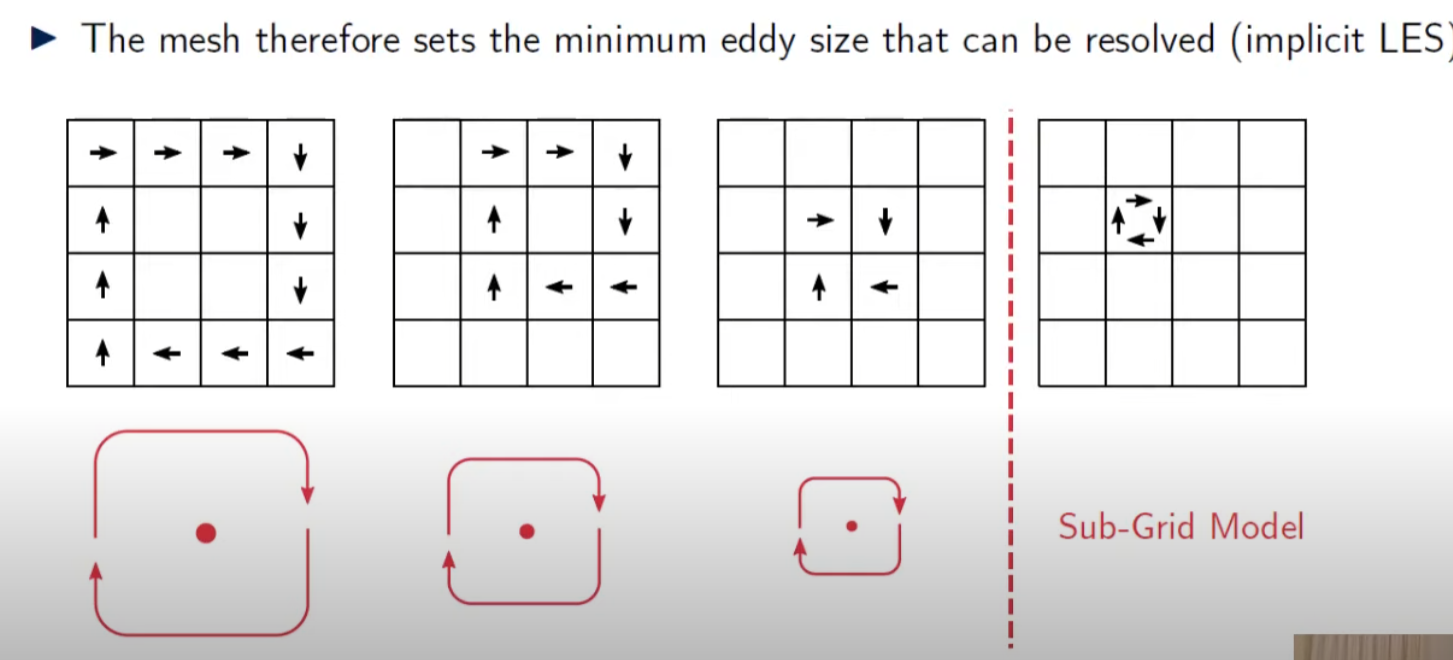 [1]
[1]
We will going to use sub-grid model that represent eddies smaller than a single mesh size
Basic Concept of Eddies
Wave number
Wave number indicates the size of the eddy. Actually, it is the reciprocal of the size of the eddy.
Wavenumber
IDK why the wavenumber is defined like this, but it is how it is.
WARNING
Turbulent Energy Cascade
This section will tell you what turbulend energy cascade is.You
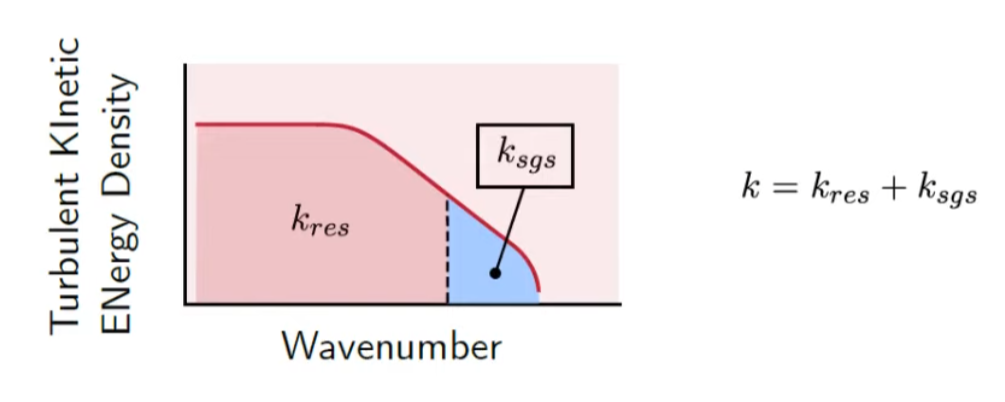
The below diagram shows the relation between the size of the eddy(wavenumber) and the kinetic energy density. 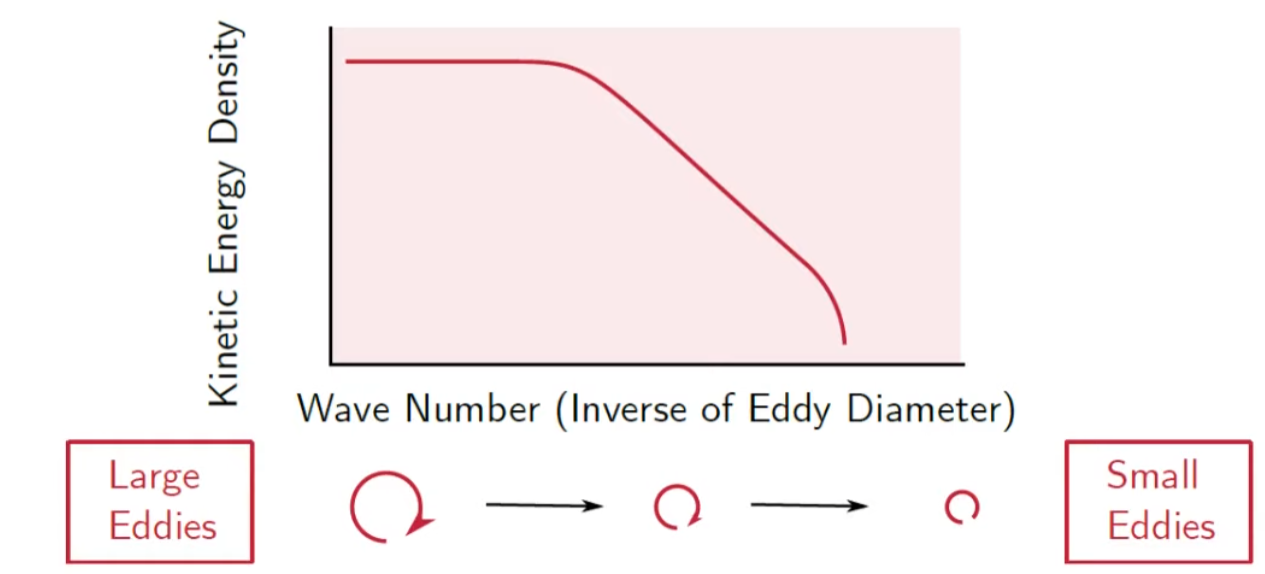
The area under the curve is the turbulent kinetic energy, TKE. 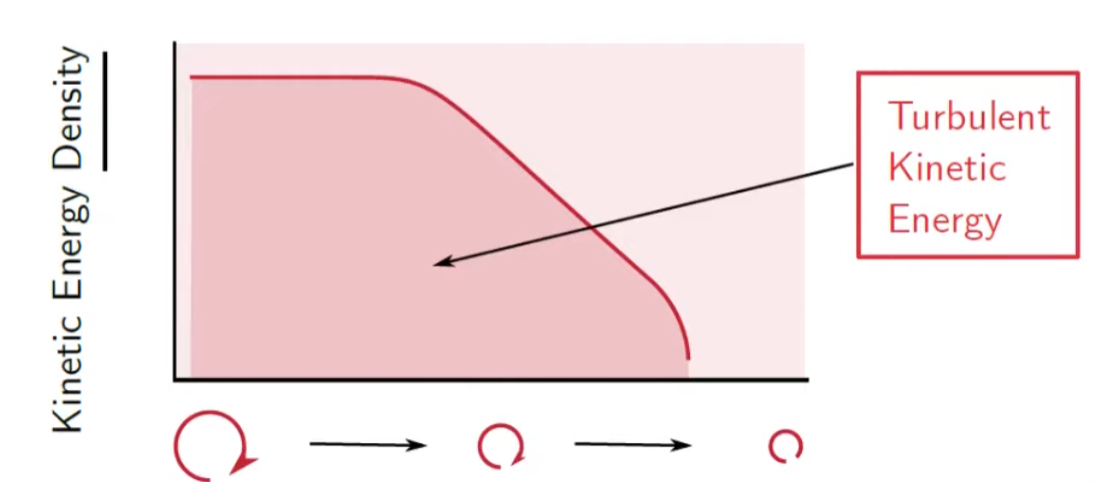
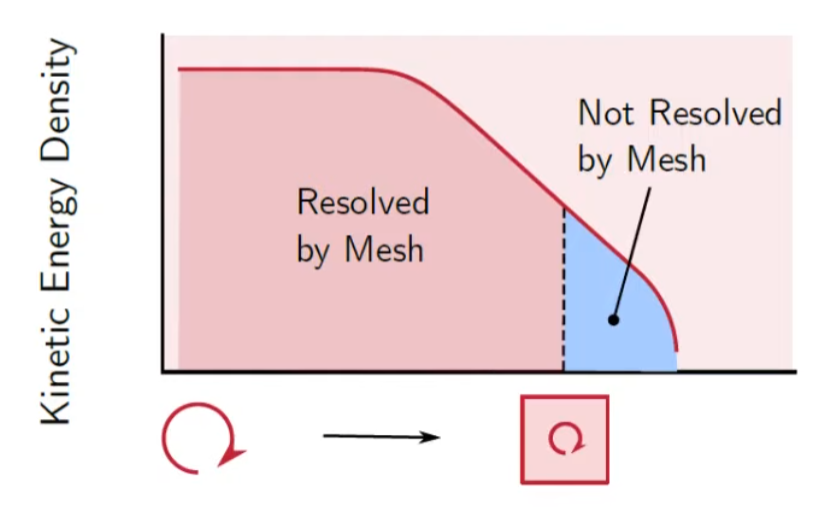 As we can't shrink the size of the mash to infinitesimal size, there's a certain point that we cannot resolve eddies using cells.
As we can't shrink the size of the mash to infinitesimal size, there's a certain point that we cannot resolve eddies using cells.
If the blue area is smaller than 20%, we call it Good LES.
IDK know why, but this is kind of convention. 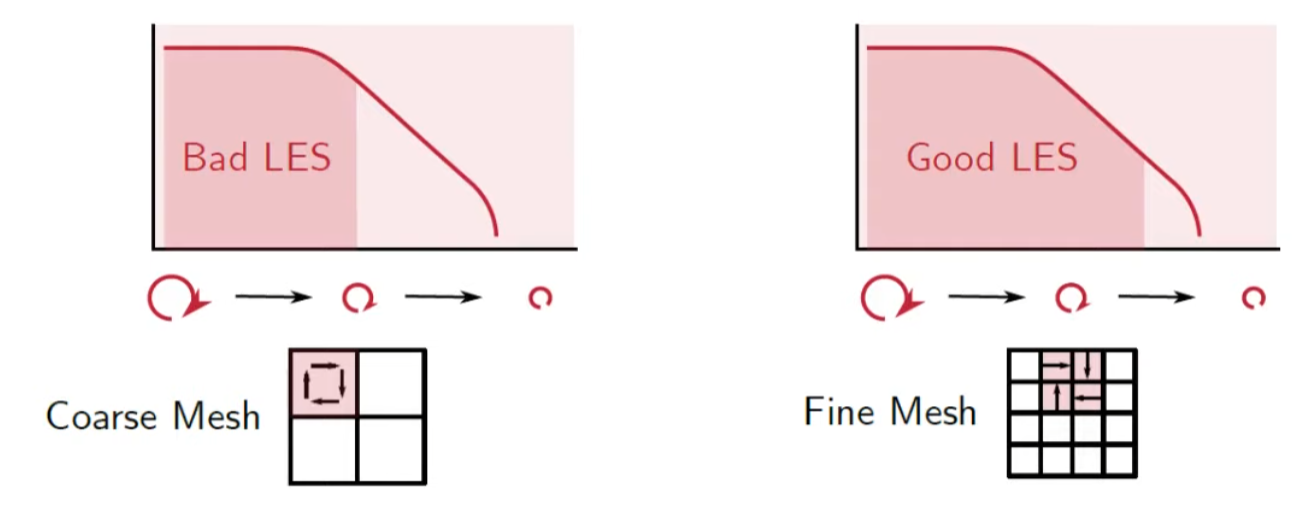
Integral length scale
The eddy size and energy will obviously vary throughout the domain. It means, each domain has different TKE, because they all have different kinetic energy density.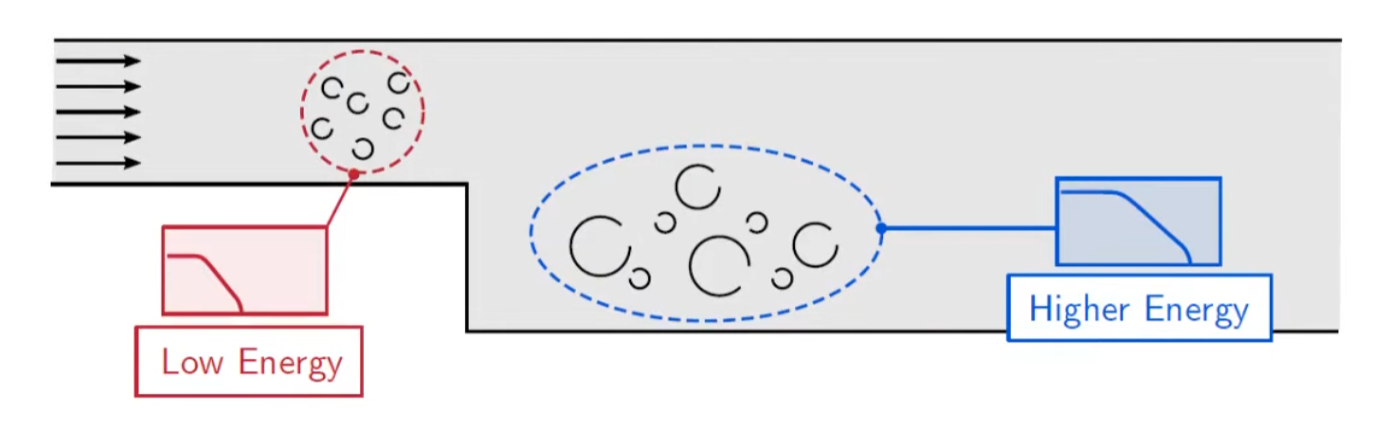
So we will have something called 'integral length scale which is representative of all the eddies at a location.
Because it is easier to look at a single value than the spectrum. 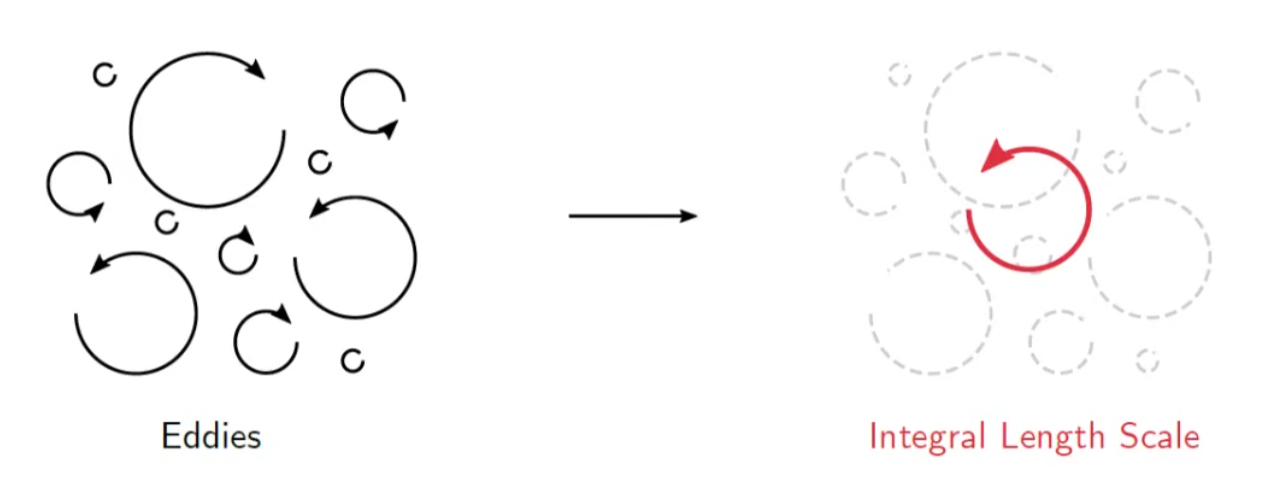
integral length scale is simply size of the averaged energy density eddy.
The area devided by integral length scale is the same.
We can calculate it by mathematical expression. 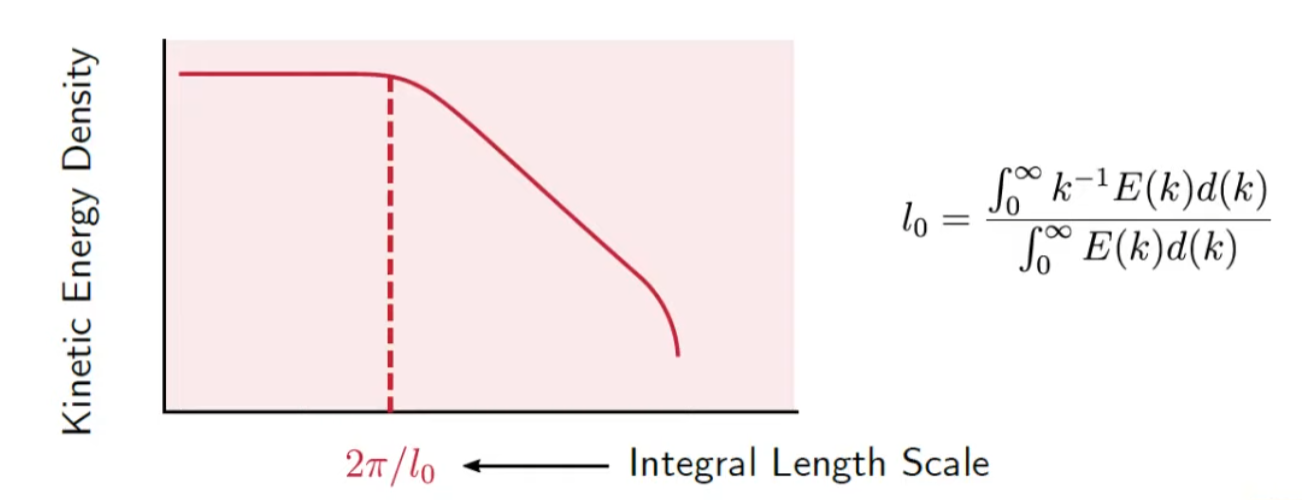
But the above mathematical expression is a bit absurd,as we don't know the function of energy density.
So how can we calculate it?
We can calculate
Question
So in order to do LES, do we have to do RANS first? what if RANS is not accurate?

We said the good LES should resolve more than 80% of energy density.
In order to to this, the size of a cell should be smaller than one fifth of the integral length scale.
So that we can resolve more than 80% of the turbulent kinetic energy. 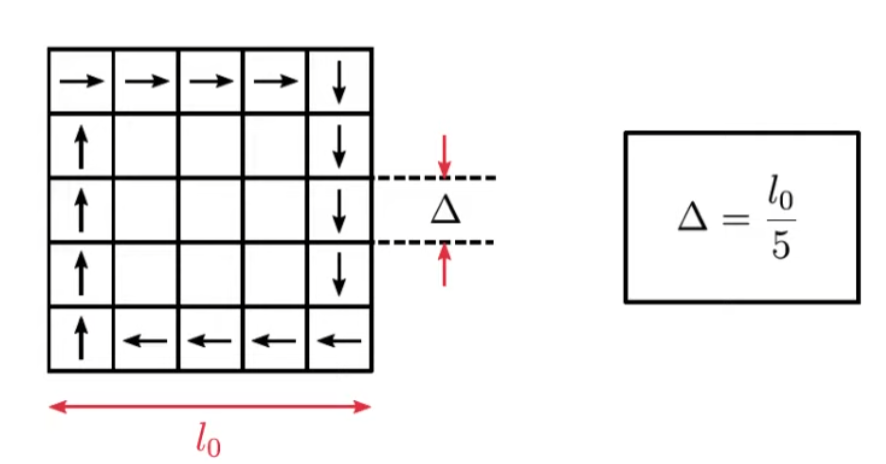
So if we want to evaluate if the mesh is good or not, we can define a new function f with variable integral length scale
How LES works - Process
0. Approach
As we discussed above, good LES should resolve more than 80% of the TKE.
So our goal is to resolve more than 80% of the TKE.
1. Calculate the Mean Velocity
First, we will going to calculate the mean velocity of the flow.
As the CFD Code computes the instantaneous velocity 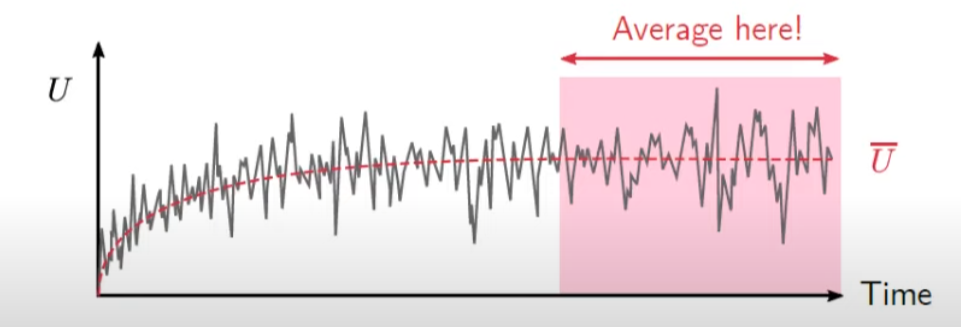
Question
How do we get U? What if U is inaccurate?
We will average the velocity after the trasient phase.
2. Fluctuating Velocity
We will do almost the same process as RANS
TIP
Difference between RANS and LES is,
RANS models the fluctuation terms using time averaged velocity terms,
But LES calculates TKE in the fluctuation terms.
As we all know, kinetic energy per mass is
So we can multiply fluctuating velocity components together, and it will lead us to some kinetic energy term.
We have three veolcity components,
There are instaneous Reynolds-Stresses that are resolved by the mesh
But, only normal components are used to calcaulte the resolved TKE.(
Question
IDK why we only use normal components for the TKE.
This is probably because of the definition of energy
And then, we time-average all those Reynolds-Stresses, and get Reynolds Stress tensor per unit density.
Question
IDK why we time-average reynolds stresses.
Anyways, we get Reynolds STress tensor per unit density.
3. Resolved Turbulent Kinetic Energy
From the diagonal components, we get resolved TKE,
just using normal components.
The reason why it is called resolved TKE is, we resolved turbulent kinetic energy only by using out mesh.
This is the best we can do here.
We can't resolve TKE smaller then a cell right now, but we will do this later.
TIP
OpenFoam will calcaulte the resolved turbulent kinetic energy directly from the mesh, adding up diagonal components.
However, in ANSYS, they will calculate
So be aware of which components you are adding up.
The image shows the rewolved TKE 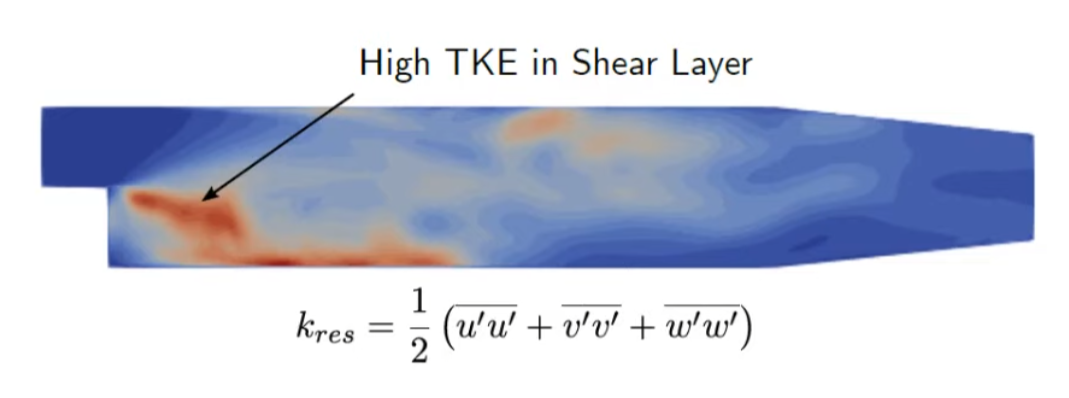
4. Total Turbulent Kinetic Energy
We now have the resolved inetic energy which is only a portion of total TKE.We still don't have sub-grid scale TKE, $k_{sgs}$
So our next goal is to get sub-grid scale TKE.
5. Sub-Grid Scale Turbulent Kinetic Energy
But how do we do this?
There are several methods like smagorinky, WALE, etc.
We will cover this later on.
But the easiest one is solving kinetic energy transport model. 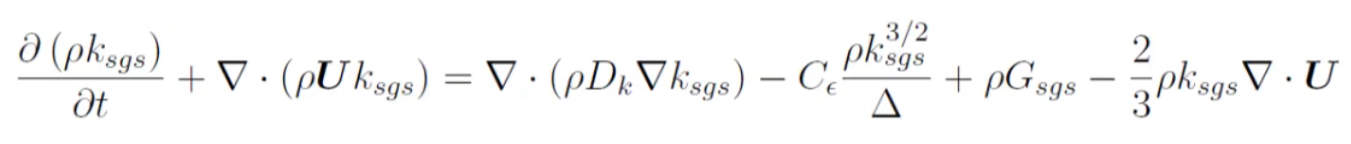
What about other methods?
One way is to calculate
$l_{sgs} represents the size of eddies within the cell. 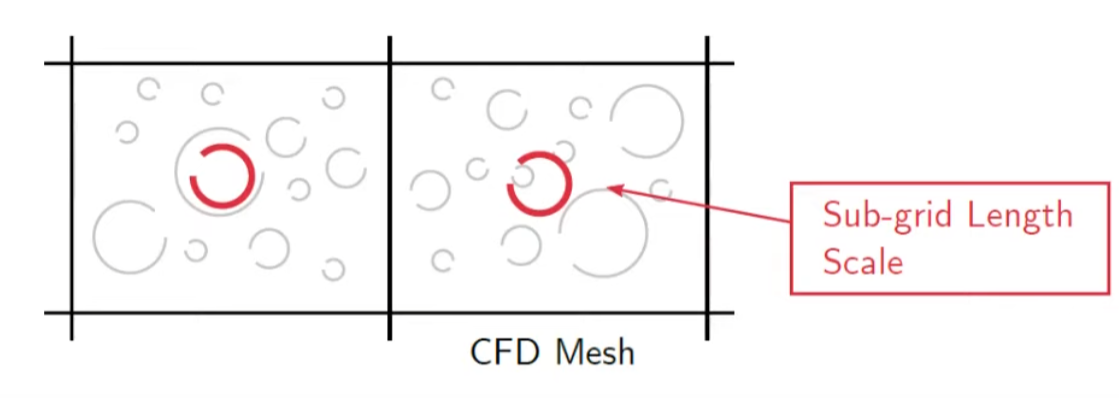
TIP
OpenFOAM calculates
6. Sub-Grid Length Scale
If
But, if we look at some of CFD mannuals, we can see that formula is slightly modified.
This is because near the walls, eddies are damped, so we modify the function.
If we are so close to the wall, we will have smaller eddies than we calculated from above.
So, modified formula is
This also represents the effect of high aspect ratio.
This will have better approximation.
7. Turbulent Kineitc Energy
Now, we have calculated
Below two picture shows 
If we want to check the quality of our CFD, we can calculate the ratio
8. Mesh Refinement
If we don't have good quality, we can refine the mesh and increase
LES Sub-Grid Model
What is Sub-Grid Model?
In LES, we looked at resolved TKE and sub-grid TKE.There are several sub-grid models, and we have to select one of those models.
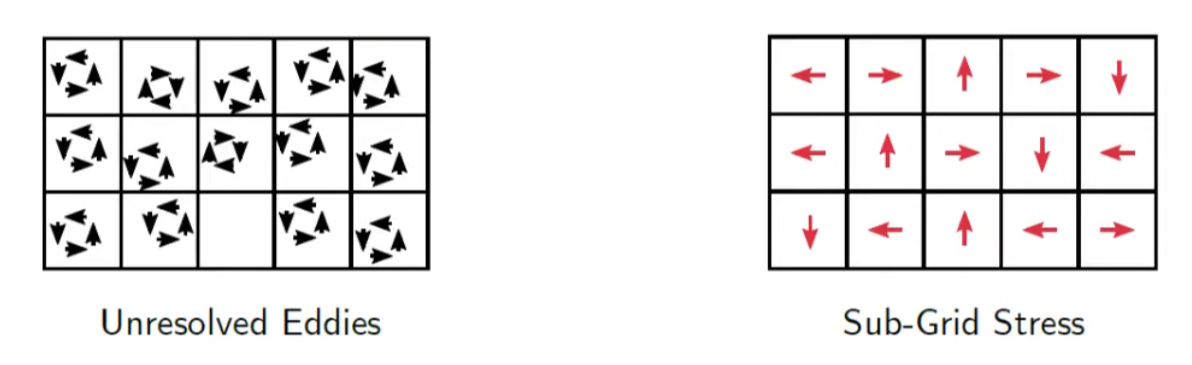
Why do we need Sub-Grid Model?
The below picture shows the reason why we need sub-grid model.In CFD Solver, the size of eddy cannot be smaller than the size of the cell, and eddies will persist and will not break down.
But we have to break it down, because that's how mother nature works.
Eddies get smaller and dissipate into heat.
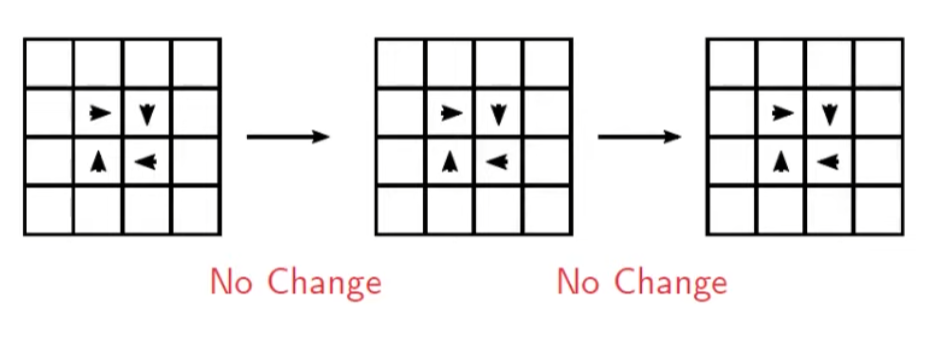
What can we do to remove eddies from the mesh?
We can do this by increasing the turbulence dissipation rate.
What is Turbulence Dissipation Rate?
Turbulence Dissipation rate,
It has units of turbulent kinetic energy per unit time.
We have large
It's quite straightforward.
Then what's the mathmatical expression?
In real turbulence,
But this is just mathamteical deifintion.
How do we calculate it?
In RANS, we solve transport equation for
But this is different in LES.
If we look at below picture, we can see that velocity gradient gets larger as eddies get smaller.
This means, at first, as velocity grdient is not large, turbulenece dissipation rate is also not large and it takes a while for the eddies to be dissipated.
However, as time goes by, eddies get smaller and velocity gradient also gets smaller and turbulence dissipation rate will accelerate.
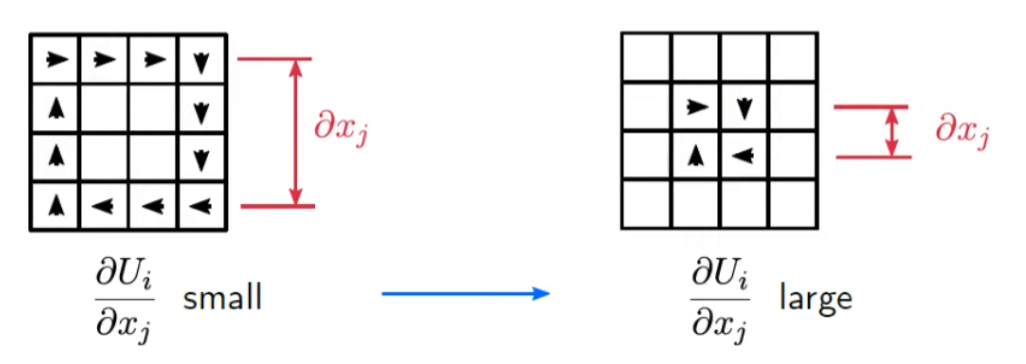
We know that eddies just bigger than the cell size are not being dissipated, and it means velocity gradient is not decreasing anymore, leading to constant turbulence dissipation rate.
But our goal is to dissipate eddies.
So, we can increase molecular viscosity
If the turbulence dissipate rate is high enough, eddies will be dissipated.
So the mathmatical expression of turbulence dissipation rate will be
If we select adequte
But we should remind that we're not solving turbulence dissipation rate in LES.
How can we reflect this concept to the real CFD?
Reminder
we're not solving
solving
And above mathematical expression is for real-world fluid.
We also have to 'model' this in LES.
Turbulence Dissipation in real LES CFD
We looked at the concept of how to dissipate eddies in LES.
But it was only a concept.
How do we increase molecular viscoity in LES simulation?
We do this by modyfing N-S equation
We can see that extra stress term
viscosity stress term
As we increased
This can be derived by filtering the N-S equation, but we'll going to skip this.
It's important to know the meaning of sub-grid stress, which is
Sub-Grid Stress
Molecular viscosity
We're going to look at the meaning of Sub-Grid Stress
If we think of eddies smaller than the size of cells, they can be considered as stresses.
Because eddies exert stresses to fluid particles and wall.
So we're substituing the concept of eddies into stresses instead of considering the real velocity of the eddies.
Sub-Grid Stress can be modeled as
And this is from eddy viscosity model.
You can find this on RANS page
If we see the equation, as the eddies get smaller, velocity gradient increases and it makes Stress tensor
But
Instead, we can control
By controlling
This also means if we have larger cell size, 
extra info
Question
Isn't the eddy viscosity model from the RANS equation?
so we use eddy viscosity model from the RANS?
Isn't the RANS inaccuarate?
Because of the cell size -
In RANS, we can change the mesh and use the same turbulence model.
But in LES, as we change the mesh, molecular viscosity
This is the characteristic of the LES.
Smagorinsky Model
As we looked at sub-grid model, we now know that sub-grid stress
And sub-grid viscosity
So how is sub-grid kinematic viscosity
There are several methods, but here, we're considering Smagorinsky model.
Expressing Sub-Grid Kinematic Viscosity Model
We can express sub-gird kinematic viscosity model as velocity multiplied by length according to the units of kinematic viscosity.
This simple approach was proposed by Smagorinky. So,
As eddies are isotropic, we only need a length
So our goal is to determine
Velocity Scale
We are going to take velocity difference 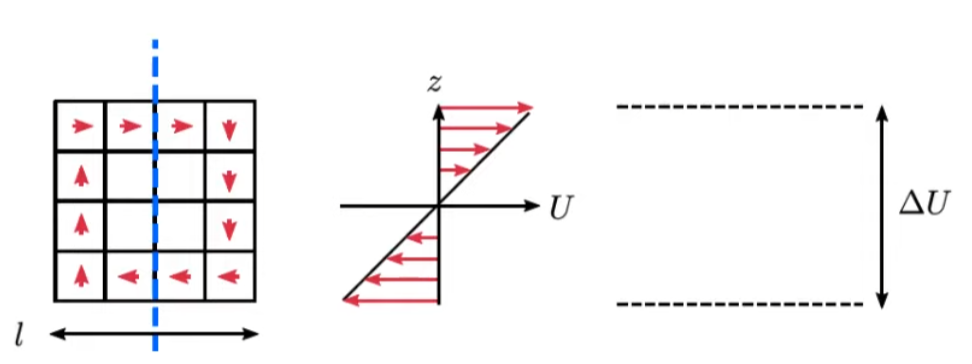
Velocity difference will be,
But what if we draw a horizontal line across the eddy?
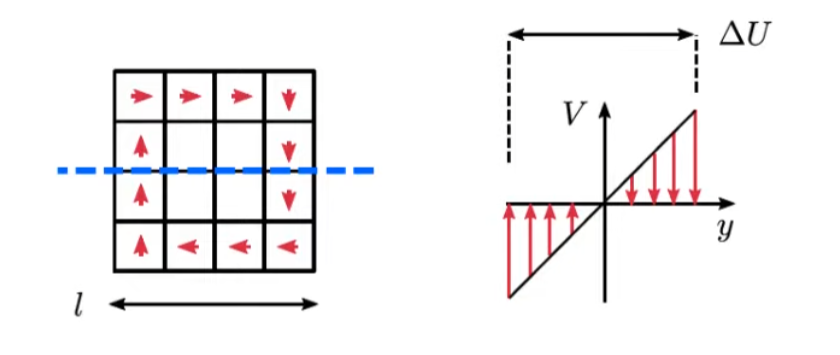
Velocity difference will be
We can express this term in strain rate tensor
But, the problem is, we need a scalar value for the velocity scale.
What if we just take magnitude of
If we look at the simple case(Couette Flow), we can know that
So we have to multiply
Problem of Simple Smagorinsky Model
Smagorinsky Model doesn't take wall effect into consideration.
Wall makes eddy small
How can we modify sub-grid kinematic viscosity to take wall effect into account?
There are several ways.
But we're only going to cover modifying
we can change
Simplest way is to modify
We can do this by using RANS equation - eddy viscosity model
Question
Still can't get it.
RANS in LES....
Why is LES accurate then?
from
And in log region, reynolds stress is constant which is wall shear stress.
From these relations, we can quantify the size of the eddy with the varient
The result will be shown in next section.
Question
why is reynolds stress constant in log region?
Quantifying the size of eddy
In logarithmic region, the mean velocity profile is modelled by
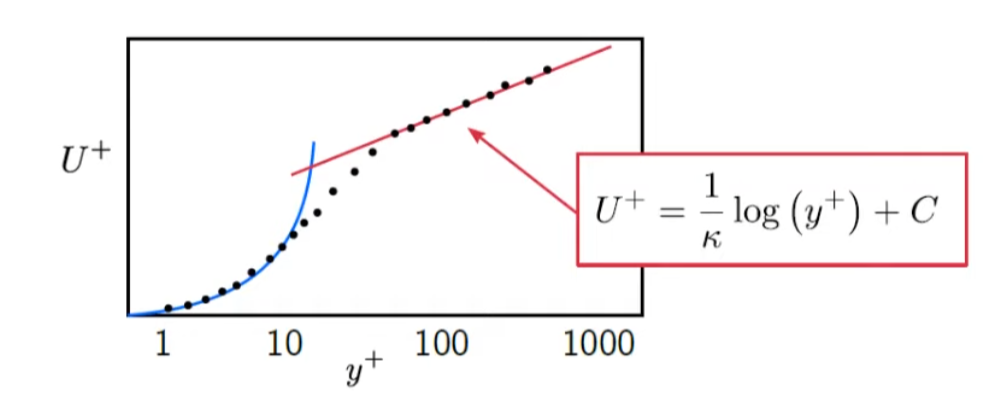 The dots are given from DNS simulation.
The dots are given from DNS simulation.
Also, in logarithmic region, Reynolds shear stress is relatively constant, hence,
TIP
But IDK the physical meaning of these terms.
So, if we plug those equations to Eddy Viscosity Equation
The Turbulent Viscosity
Turbulent Viscosity
So what will be the adequate choice for
Question
I'm not sure about how
Anyways, if we massage the equation, we get
So what does it mean?
As we get close to the wall,
So this is the behavior that we wanted.
Taking wall effect into account.
Now we will return to where we start from, modeling sub-grid scale molecular viscosity
Revisiting Sub-Grid Scale
Now we have more accurate model for the sub-grid scale eddies.
So when modeling sub-grid length scale
But our
How can we consider other region?
We can do this by using Van Driest Solution.
We can get general equation that rerpresent relation between 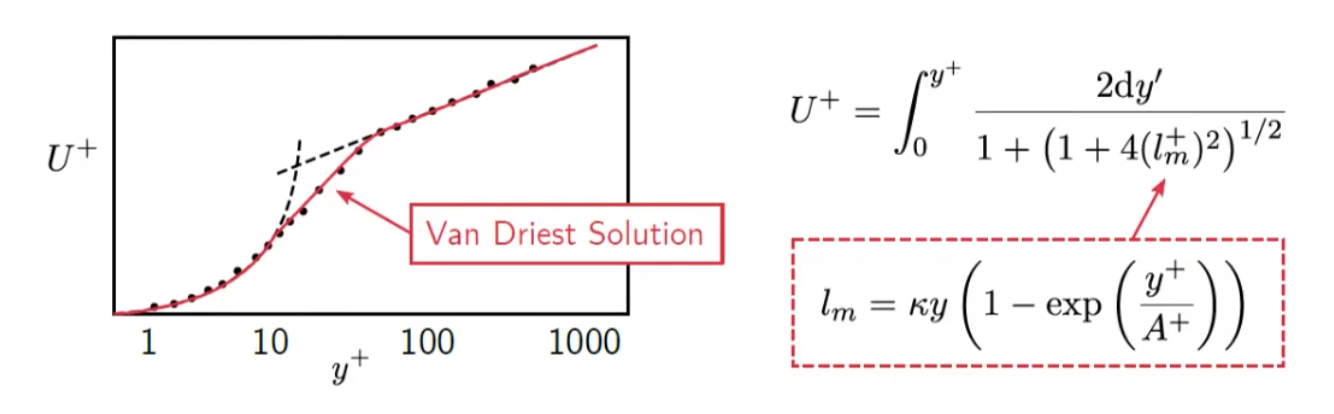
So the final Sub-Grid Length Scale will be
Summary of LES
In LES, we have to solve to parts.
- Resolving larger-than-grid-size-eddies turbulent kinetic energy
These values can be solved with 100% accuracy. And it is better to resolve TKE as much as possible. - Modelling Sub-grid-sclae Turbulent Kinetic Energy.
This is the trickies part of LES.
We used turbulence dissipation rate
By physical definition of
But in real CFD, we can't use this.
In order to solve in real CFD, we will use N-S equation to reflect the same phenomenon.
We can do this by modifying viscost stress term
And
If we control
So how is
We can do this by using Smagorinsky model, which models
Next step is to model length scale
The simplest approach is to add some Coffecient to the cell size because sub-grid eddies is smaller than the size of the Cell.
So,
And C_s is Sagorinksy Coefficient.
But the problem is, it cannot take wall effect into account.
Eddies will get smaller as they approach the wall.
So, we use reynolds stress to model this.
Question
This is the huge missing link of LES.
Why do we use RANS eddy viscosity model to LES?
Why does this work?
Anyways, if we do some simple math with RANS eddy viscosity model, we get mxing length as the resprentative of size of the eddies.
So as a result we get sub-grid length which represents the size of sub-grid eddies as,
And this takes wall effect into account.
I will resummary the above summary. sub-grid length scale